An Odyssey

在生成迷宫的诸多方法里，有一种思路是假设迷宫初始状态是由长×宽个独立单元格构成的，每个单元格的东西南北四个方向都有可以挖掉的墙。生成迷宫的过程就是从起点开始，不断挖掉两个单元格之间的墙壁，并随机选择前进方向直到遍历全部单元格，这样就能保证起点和另外任何一个单元格都有通路存在，迷宫也就生成好了。

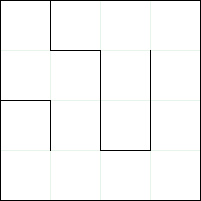
本文想介绍的是，在我们使用上述方法生成好描述迷宫的数据后，除了用字符在终端里输出外，还可以通过canvas方便且美观地在浏览器环境绘制迷宫。

Processing

Processing是一种绘图语言，它在程序起始时运行一次初始化环境，然后不停循环draw()函数来描述动画每一帧要做什么。Processing设计思路和Arduino非常像，流程清晰可控而且易于上手。ProcessJS作为其衍生项目也继承了这种优点，你甚至可以直接在html里书写Java风格的代码，这提供了非常好的代码移植性，只要将代码放在<script type="text/processing" data-processing-target="mycanvas"></script>标签内即可。

数据格式

我们绘图用的数据源是下面这种二维数组的形式：

[[2,4,14,10],
[5,10,3,3],
[2,3,1,3],
[5,13,12,9]]

这是一组回溯递归法产生的数据，首先定义每个单元格的东西南北4个方向为N=1，S=2，W=4，E=8

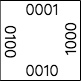
这样定义的原因是便于标记每一步的行走方向，1、2、4、8转换成二进制恰好是0001，0010，0100，1000的One Hot编码格式。比如说初始状态每个单元格都被标记为0000，然后我们向南走一步，就是用代表东的0010与初始状态0000作位或运算0000|0010=0010，得到0010作为新的状态，然后我们再向东走一步，0010|1000=1010，最终得到1010，我们就知道这个单元格曾经有南和东两个方向的路径。

初始化绘图环境

下面介绍绘图环境的初始化：

void setup() {  
    sideLength = 301;
    size(sideLength, sideLength);
    background(255);
}

其中size()函数用来定义canvas画布大小，background(255)设置背景颜色为白色。由于迷宫是静止的，所以只需在在click事件里加一句回调Processing.instances[0].maze(data);运行一次自己定义的函数就好了。

我首先用淡色描出了迷宫的网格，这能让迷宫看起来规整一些。每次运行都要重新设置背景来清空上一次的图形，用val || default_val设置边长的默认参数，然后计算每个网格的宽度step。用stroke()设置线条颜色，width是存储canvas画布宽度的全局变量，line(x1, y1, x2, y2)画出一条从(x1, y1)到(x2, y2)的直线。这里要注意像素坐标原点在canvas的左上角(0, 0)，所以只能画到width-1的位置。

void maze(g) {  
    background(255);
    rows = $("#row").val() || 15;
    cols = rows;
    step = (width-1)/rows;
    stroke(137, 194, 148, 50);
    for(int i=0; i<=width-1;) {
        line(i, 0, i, width-1);
        line(0, i, width-1, i);
        i+=step;
    }
}

绘制迷宫

然后就是根据数据绘制迷宫，因为正方形存在两对对称关系，当上方/左方的单元格开口方向确定后，相应的下方/右方单元格的开口就确定了，所以我们只需要处理每个单元格的S和E方向就行了，最后剩下迷宫的上边框和左边框没有处理，我们再画上两条长线。

与生成迷宫的或运算相反，如果某一格与0010（南）或运算的结果为0 (g[i][j] & 2) == 0)，这说明生成这一格时并没有向南走，也就是说这一格南面有一堵墙，我们就在这一格下方画一条线line(step*j, step*(i+1), step*(j+1), step*(i+1));。

同理，如果(g[i][j] & 4) == 0)，东面有墙时也是如此，当全部单元格都遍历到后，迷宫也就绘制完了。

效果

全部代码如下：

stroke(0);  
line(0, 0, width, 0);
line(0, 0, 0, width);
for(int i=0; i<=rows-1; i++) {
    for(int j=0; j<=rows-1; j++) {
        if((g[i][j] & 2) == 0) {
            line(step*j, step*(i+1), step*(j+1), step*(i+1));
        }
        if((g[i][j] & 4) == 0) {
            line(step*(j+1), step*i, step*(j+1), step*(i+1));
        }
    }
}

具体效果可以在这里查看：